1 Introduction
1.1 Precedence and Studieveld
2 Attributive and relational classifications
2.1 Two ways of classification
2.2 Attributive classification
2.3 Relational classification
2.4 Explanation
3 Kinship in Ende
3.1 Introduction
3.2 Patrilineality as attributive classification
3.3 WG/WT as Relational Classification
4 Precedence and hierarchy
4.1 Two kinds of dualism
4.2 Conversion with Age
The idea of `precedence' is closely connected with that of the `studieveld' (`study field') (Fox 1980) (of eastern Indonesia or perhaps Austronesian world). In this sense, it is an ``experience-near'' category (Geertz 1983).
Concerning its closeness to the idea of `study field', there arise two features about `precedence' as an analytical notion: one good and the other bad.
Good news is that the notion of `precedence' goes well with other items derived from the same study field. The notions such as ``origin'', botanic metaphors etc fit well with `precedence'. Sometimes we even find a native notion of `precedence' (oda in Tana 'Ai (Lewis 1988).
Bad news is that it (the notion of `precedence') tends to lose its beauty when combined with other `analytical notions' derived from other study field, especially `hierarchy' (derived from South Asia (Dumont 1970). For this `precedence'/`hierarchy' problem, we have to remember Greg's beautiful paper, ``Distinguishing hierarchy and precedence'' (Acciaioli 2009). He spent tremendous efforts for tackling this problem, quoting varous ethnographic data.
In one's field, one finds a lot of asymmetric relations. and one tends to wonder which is Precedence and which is not.
In my field (Ende in Flores) it is WG/WT relation and AG/AG (agnates) relation that baffle me most. Both can be said to be Precedence (see, for example, (Butterworth 2008)) but they are of quite different natures.
My aim of this paper is to propose another pair of analytic tools, this time, ``experience-distant''one, to be coupled with ``experience-near'' precedence so that they, coupled together, can shed lights to `precedence'/`hierarchy' problem.
In a way, this paper is meant to be a complementary essay to Greg's. He tried to elucidate the idea of precedence from below (as it were), while I try to do the same from above (as it were).
My starting point is to regard `precedence' as a kind of classification and, thus, I wish to build a more primitive kind of typology of classification here (than `precedence').
Without further ado, I contend that classification consists of (1) identification (sameness) and (2) differentiation (difference). Accordingly, there are 2 kinds of classification: (1) one based on sameness and (2) another on difference.
The former, I call ``Attributive classification'' in which sameness is given and difference is to be inferred; the latter, ``Relational classification'' in which difference is given and sameness is what is to be inferred.
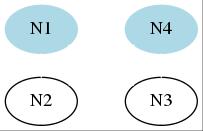
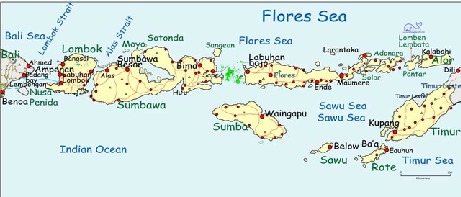
Now let us start with the attributive classification. Attributive classification is one where each node's attribute is given and the relation is what is to be inferred.
See the diagram below which
shows a original situation of
attributive classification.
Each node has already have its own
attribute,
here, colour.
Some are painted blue,
Some white.
Note also that
there has not been relations
between nodes defined yet.

What we have to do is to produce relations from this original situation. There are two rules for attributive classification: (1) Connect differently coloured nodes with a line, and (2) Use as many lines as possible.
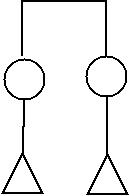
See the diagram below for the resultant
situation.
The attributes (that is, colours) had been
alloted to the nodes;
now the relations
(that is, lines) have
been drawn according to the two rules.
It is complete now.
Thus, in attributive classification,
sameness produces difference.
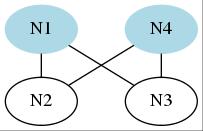
In relational classification, on the contrary, the relation between nodes is what is given and each node's attribute is what is to be inferred.
Below is the original situation of
the relational classification.
Here you can ses
relations (that is, lines)
have been drawn between nodes.
But no nodes has its attribute
(that is, colour)
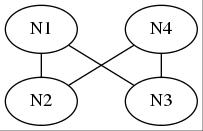
Now our task is to procure attributes in this original situation. There are two rules: A main rules is: (1) Paint connected nodes in different colours and a auxiliary rule is: (2) Use as few colors as possible.
See the figure below for the result.
Relations (lines) had been drawn.
Now each node has been given its own attribute
(colour)
according to the rules.
Thus, differece produces sameness
in relational classification.

The two resultant diagrams are, as you can see, exactly the same; but the difference comes when one tries to explain how come the diagrams have been made.
First about attributive classification.

In attributive classification, Difference is explained by Sameness (which is the given in this system). (Difference) Why are N1 and N2 connected? Because they are differently coloured (Sameness) Why are N1 and N4 of the same colour? ... (!?) (it's given)
How about relational classification, now.
See the diagram below.
Remember,
first, attributes have been given;
and it is only later that
relations are made
according the rules and the pattern of
attribute.

In relational classification, Difference produces sameness; in other words, sameness is explained by difference (the given). In this system, you can answer easily such questions as ``Why are N1 and N4 of the same color?'' You just say: Because they are connected in such a way that accord with the rules. This explanation will be discussed in details later.
On the other hand, you cannot answer questions such as ``Why are N1 and N2 connected?'' because relations are what have been given already. It (difference) is not something to be explained in this sysmtem; it's a given.
The explanation needs a bit more clarification, I suppose. The best and shortest way of saying that N1 and N4 are of the same group is using (what I call) ``enemy's enemy principle''. In our lives, one's enemy's enemy sometimes proves to be one's friend. Let's assume that connecting lines represent `enemy' relations. Thus, N2 is an enemy of N1 and N2 is also an enemy of N4, and N1 and N4 become friends.
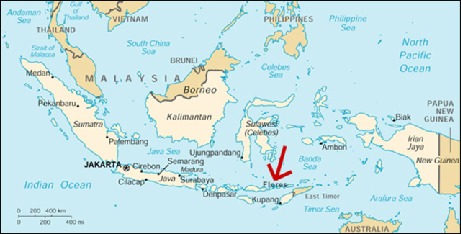
Now it's Ende time.
Ende people live in the central part
of Flores.
Ende is a patrilineal society,
with the idea of asymmetric alliance
(mother's brother's daughter's marriage).
Ende is a patrilineal society;
and patrilineality is the typical example
of the attributive classification.
Patrilineally related members are regarded as of
one and the same group.

Now, let's read connected lines as marriageability. And parallel to the Q and A I mentioned above, the following Q and A will ensue: Why do N1 and N2 marry? Because they are different. Why are N1 and N4 of the same group and there will be no answer.
This is, incidentally, ``descent theory''

Next, about Relational classification in Ende.
It is WG/WT relationship that is
the Difference relation
in Ende,
in the sense that
WGs (or WTs for that matter)
are the archetypal ``other''.

It should be noted, in this connection, that
In Ende, not only patrilateral
parallel cousins (FBS/FBS),
but also matrilateral parallel
cousins (MZS/MZS)
are regarded as ``adik kakak''
(ari ka'E.
It is obvious that FBS/FBS are regarded
as ``adik kakak'' (``brothers'')
once we remember the patrilineality
principle in Ende.
But the case of MZS/MZS
needs more to be explained.
It is enemy's enemy's principle also that
plays its part in establishing sameness
from difference

Now we come to `precedence'.
In his article in which he introduced the notion of `precedence' (Fox 1989), Pak Jim mentions the 3 features of precedence as: (1) categorical asymmetry, (2) recursive complementarity, and (3) (the possibility of) category reversal. In a later paper (fox-discourse_and_practice), he adds (or rather, summarises) that in `precedence', one term accorded a value over the other.
What I want to emphasize here is that `precedence' is about `value' And, just don't forget, so is `hierarchy'. Two ways of classification, on the other hand, has nothing to do with value. Precedence is content Classification is form
The problem now is how we can bridge the value-free classification (which I have discussed so far) with the value-laden precedence and hierarchy.
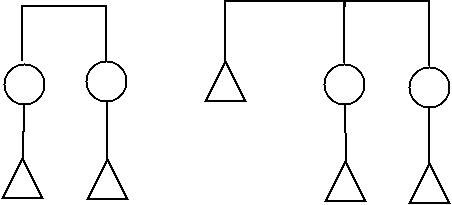
The
One of the points of the paper is that one and the same village is represented, sometimes as forming a diametric dualism, and sometimes as forming a concentric dualism. One can see a phenomenon, sometimes as (value-free) classification sometimes as (value-laden) precedence (and hierarchy). It is by changing way of seeing things which introduces the value in the system; by changing the diametric to the concentric dualism.
Let's see how it can be done

Attributive and concentric system is `precedence' whereas relational and concentric system is `hierarchy'. I'm not sure ...; Ask Greg whether this is correct
... Anyway ....
| Attributive | Relational | |
|---|---|---|
| Diametric (value-free) | --- | --- |
| Concentric (value-laden) | precedence | hierarchy |
Now let's go back to the Ende ethnography
to see how the conversion from
value-free classification to value-laden
system (precedence and hierarchy).
It is
Very briefly, it is that in a lineal descent system categories will be preponderant, whereas in a cognatic society there will be a lesser emphasis on categories in favour of social distinctions based most generally on relative age. (Needham 1966: 31) ,Needham on Age, Category and Descent
In this final section, to simplify the matter, I'll limit my discussion to ``adik kakak'' (parallel sibling) relations alone. Further more, among them, I'll deal with only cases of brothers on the one hand and sisters on the other.
In Ende, ``adik kakak'' relationship is, more or less, egalitarian; but sometimes, values are added to one over the other, more often in case of brothers than in sisters.
This granting of value is
emphasized by converting difference
of
Nothing substantial happens
when eB/yB relation is converted to F/S.
It is not the case with eZ/yZ
conversion to M/D relation;
since M/D relation is actually a WG/WT
relation .

In conclusion, I would say that, in Ende, there are two types of value-laden relations: one is `precedence' represented as patrilineality and the other is `hierarchy' represented as matrilineality (or WG/WT relationship).
| Attributive | Relational | |
|---|---|---|
| patriliny | matriliny | |
| Diametric | (FBS/FBS) | (MZS/MZS) |
| Concentric | Precedence (eB/yB) | Hierarchy (WG/WT) |
